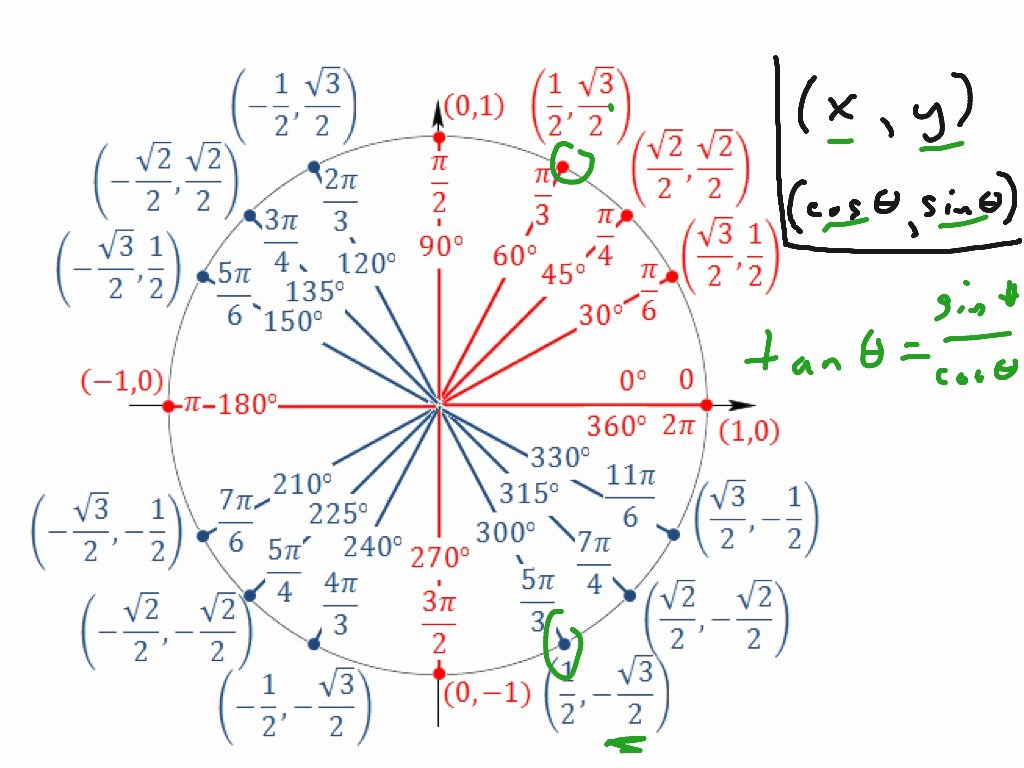
The result is a right triangle △ORS with ∠SOR = t. Now consider a point S(− x 1,0) and line segments RS ⊥ OS. Having established these equivalences, take another radius OR from the origin to a point R(− x 1, y 1) on the circle such that the same angle t is formed with the negative arm of the x-axis. Because PQ has length y 1, OQ length x 1, and OP has length 1 as a radius on the unit circle, sin( t) = y 1 and cos( t) = x 1. The result is a right triangle △OPQ with ∠QOP = t. Now consider a point Q( x 1,0) and line segments PQ ⊥ OQ. First, construct a radius OP from the origin O to a point P( x 1, y 1) on the unit circle such that an angle t with 0 < t < π / 2 is formed with the positive arm of the x-axis. Triangles constructed on the unit circle can also be used to illustrate the periodicity of the trigonometric functions. When broken into real and imaginary components z = x + i y, z=x+iy, this condition is | z | 2 = z z ¯ = x 2 + y 2 = 1. This is the set of complex numbers z such that | z | = 1. In the complex plane, numbers of unit magnitude are called the unit complex numbers. Main article: unit complex numbers Animation of the unit circle with angles